The Balmer-Rydberg Equation calculator computes the wavelength corresponding to the hydrogen atom's energy level differences when an electric current is passed through hydrogen gas at a low pressure.
INSTRUCTIONS: Enter the following:
- (n1) Higher energy state for a spectral emission (integer)
- (n2) Lower energy state for a spectral emission (1 is the lowest).
Wavelength (λ): The calculator returns the wavelength (λ) in units of nanometers (nm). However this can be automatically converted to other length units (e.g. angstroms) via the pull-down menu.
The Math / Science
The differences between energy levels are equal to the energy emitted or absorbed as photons when an electron transitions from a higher energy level to a lower quantum energy level. The Balmer-Rydber equation is as follows:
λ = 1 / [R ((1/n2) - (1/n'2))]
where:
- R is the Rydberg constant (1.097x 107 m-1)
- n1 is the integer number of the higher energy state for a spectral emission
- n2 is the integer number of the lower energy state for a spectral emission (1 is the lowest).
- λ is the wavelength
The formula computes the wavelengths corresponding to the hydrogen atom's energy level differences when an electric current is passed through hydrogen gas at a low pressure. The differences between energy levels are equal to the energy emitted or absorbed as photons when an electron transitions from a higher energy level to a lower quantum energy level.
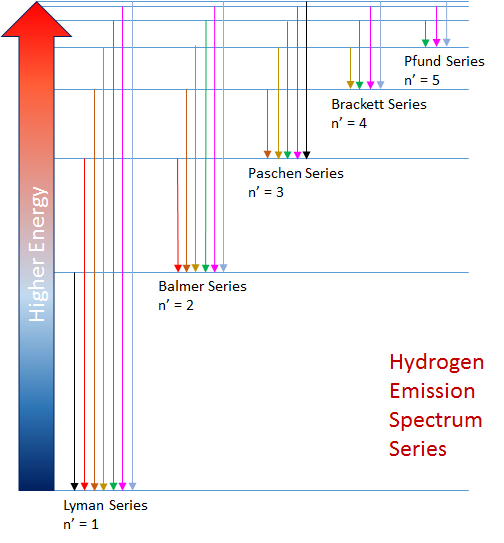
When an electric current is passed through hydrogen gas (contained in a thin tube) at low pressure, a pink glow results. If this light is passed through a grating, more colors will result and this is considered to be hydrogen's emission spectrum. The emission spectrum for the transitions between all the energy levels of the hydrogen atom are partitioned into groups of transitions or spectral series, where the lower energy state in any transition, n', characterizes the spectral series. The energy states, created by the electromagnetic forces between electrons and protons in the atom, are fixed. This ensures the hydrogen spectrum is always emitted at the precise wavelengths defined by the Rydberg Equation. The graphics above show the first five of an infinite number of spectral series for the hydrogen atom.
The Balmer-Rydberg equation calculates the wavelength of a specific line in the hydrogen emission spectrum. In 1885, Balmer created an equation to determine the wavelength for individual lines in the Balmer Series, which Rydberg later generalized so that it could be used to find the wavelength of any of the lines in the hydrogen emission spectrum.
See Also
UCDavis ChemWiki: Hydrogen's Atomic Emission Spectrum
References
Whitten, et al. "Chemistry" 10th Edition. Pp. 139